Modellierung von Leiterplattenverbindungen als kausale Systeme

Jeder, der irgendetwas über Albert Einstein gelesen hat, hat schon einmal das Wort "Kausalität" gehört. Zwar wird über Kausalität meistens im Zusammenhang mit der Relativitätstheorie und Quantenmechanik gesprochen, aber die grundsätzliche Idee ist für jedes dynamische System zentral. Leiterplattenverbindungen sind kausale Systeme, und die genaue Modellierung einer Leiterplattenverbindung erfordert die Berücksichtigung bestimmter Aspekte des Signalverhaltens und der Reaktion des Systems.
Wenn Sie das kausale Verhalten Ihrer Signale korrekt modellieren, können Sie die richtige Reaktion in einer Verbindung berechnen. Dies ist entscheidend für die korrekte Vorhersage der Verbindungsimpedanz, der Impulsantwort und der Verluste. Alle diese Aspekte des Signalverhaltens sind bei Hochgeschwindigkeitsverbindungen, bei denen die Signalbandbreiten leicht in den GHz-Bereich reichen, von entscheidender Bedeutung.
Kausale Systeme und Kausalmodelle
Kausale Systeme sind so definiert, dass sie erst auf einen externen Stimulus reagieren, nachdem der Stimulus aufgetreten ist, und nicht vorher. Solange das Verhalten im Frequenzbereich und im Zeitbereich richtig definiert ist, erzeugt das Standard-Übertragungsleitungsmodell mit vereinzelten Elementen eine kausale Signalantwort, wenn die Leitung angesteuert wird. Der kritische Aspekt hierbei ist die Modellierung einer Verbindung mit einer Amplitude von Null vor t = 0. Mit anderen Worten: Sie verwenden eine Heaviside-Sprungfunktion als Gewichtungsfunktion für Ihr injiziertes Signal.
Ich persönlich arbeite lieber in der Laplace- oder Fourier-Domäne, da hier die Transformationen für eine breite Palette von Funktionen leicht zu definieren sind. Die Standardtechnik zur Berücksichtigung der Kausalität besteht darin, die Übertragungsfunktion in einer der beiden Domänen für eine Verbindung in Form der gewünschten Impulsantwortfunktion oder Sprungantwortfunktion des Systems zu bestimmen. Umgekehrt gilt: Wenn die Übertragungsfunktion eines Systems nicht korrekt definiert ist, können die Impuls- und Sprungantworten ein nicht-kausales Verhalten aufweisen - das heißt, das Signal breitet sich auf einer Verbindung aus, bevor der Treiber schaltet!
In der Signalverarbeitung ist dies seit Jahrzehnten bekannt, aber auch die Leiterplattenentwickler sollten sich dieser potenziellen nicht-kausalen Probleme bei der Modellierung des Verbindungsverhaltens bewusst sein. Die Beziehung zwischen der kausalen Übertragungsfunktion einer Verbindung (Fourier-Domäne) und ihrer Impulsantwortfunktion h(t) ist:
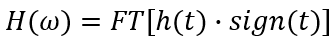
Wenn Sie also die kausale Impulsantwortfunktion kennen, die Sie für Ihr System benötigen, können Sie die Übertragungsfunktion des Systems berechnen; dies würde mithilfe des Faltungstheorems erfolgen und ein Paar Kramers-Kronig-Beziehungen ergeben. Achtung: Wenn eine Übertragungsfunktion für eine Verbindung bekannt ist, können Sie die Impulsantwortfunktion h(t) mit einer inversen Fourier-Transformation wiederherstellen und überprüfen, ob sie tatsächlich kausal ist. Eine falsche Modellierung der Übertragungsfunktion einer Verbindung (d. h. wenn die Übertragungsfunktion nicht kausal ist) führt zu einer falschen Modellierung des Signalverhaltens. Dieses Problem wird normalerweise erst ersichtlich, wenn Sie mit Signalbandbreiten jenseits von ~5 GHz arbeiten. Dies soll verdeutlichen, wie wichtig es ist, die Impulsantwort einer Verbindung korrekt zu beschreiben. Hierfür sind genaue Impedanzberechnungen als Funktion der Frequenz bis weit in den GHz-Bereich hinein erforderlich.
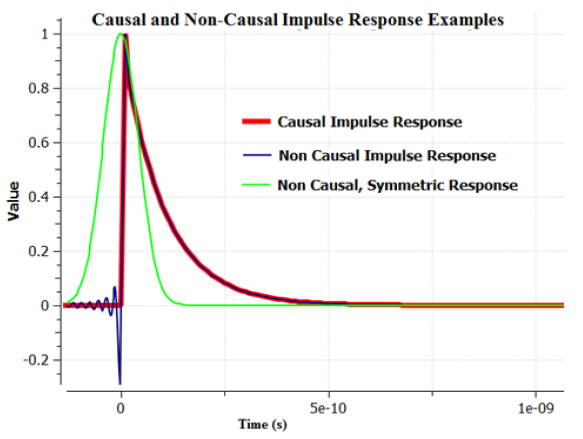
Kausalmodelle für die Impedanzsteuerung
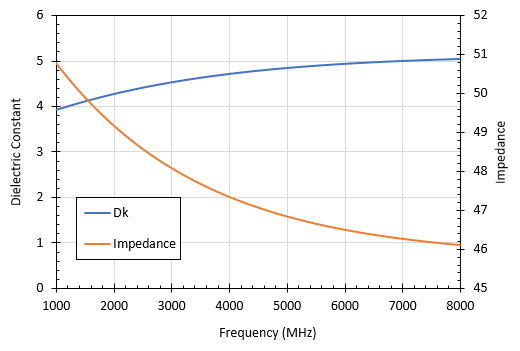
Eine genaue Impedanzsteuerung bei einer bestimmten Frequenz erfordert eine genaue Modellierung der Dielektrizitätskonstante in einem kausalen System. Wenn Sie über einen ausreichend breiten Frequenzbereich schauen, wird jedes Material eine gewisse Dispersion aufweisen. Ein vollständiger Datensatz über den Real- und Imaginärteil des Brechungsindexes kann über einen breiten Bereich schwer zu finden sein. Angenommen, Sie haben Zugang zu diesen Daten, entweder aus der Literatur oder aus Messungen. In diesem Fall können Sie diese Werte verwenden, um die Impedanz zu berechnen, z. B. die effektive Dielektrizitätskonstante, die von einem Signal gesehen wird, das auf einer Mikrostreifenleitung über einen breiten Frequenzbereich läuft.
Damit erhalten Sie dann die charakteristische Impedanz der Leiterbahn bei vorhandener dielektrischer Dispersion. Ähnliche Verfahren können für andere Übertragungsleitungsgeometrien verwendet werden. Unabhängig davon, ob Sie die Impedanz aus der effektiven (frequenzabhängigen) Dielektrizitätskonstante mit einer Standard-Impedanzformel für Leiterbahnen (Microstrip oder Stripline) berechnen oder ob Sie die Störeinflüsse in Ihrer Leiterplatte als Funktion der Frequenz extrahieren: Sie können die charakteristische Impedanz als Funktion der Frequenz berechnen. Zusätzlich benötigen Sie die Verluste als eine Funktion der Frequenz. Dies ist intuitiver, wenn Sie sich die Störeinflüsse in Übertragungsleitungsmodellen ansehen und die Frequenzabhängigkeit der Störeinflüsse berechnen. In diesem IEEE-Artikel erhalten Sie einen guten Überblick über die Modellierung des Verhaltens von Störeinflüssen als Funktion der Frequenz.
Die Alternative ist die Verwendung eines Modells das den Frequenzgang des Dielektrikums (sowohl den Real- als auch den Imaginärteil) in Form einer kleinen Anzahl von Messungen definiert. Die typische Methode, die im Unterricht der Laserphysik und der Signalverarbeitung gelehrt wird, ist die Verwendung der Kramers-Kronig-Beziehungen, um Real- und Imaginärteil einer Materialeigenschaft, einer Übertragungsfunktion oder des Signals selbst in Beziehung zu setzen. Dieses Paar gekoppelter Integrale wird verwendet, um die kausale Antwort eines Systems zu definieren, wenn die Verluste im System bekannt sind, oder alternativ, um die Verluste zu berechnen, wenn die kausale Antwort im System bekannt ist. Die andere Methode besteht darin, ein Standardmodell zu verwenden, das ein Anpassungsprofil für die relative Dielektrizitätskonstante definiert; die Parameter, die die Anpassungskurve definieren, werden dann aus einer begrenzten Anzahl von Messungen bestimmt. Für die Modellierung der Dispersion in Leiterplattensubstraten, insbesondere PTFE-Laminaten und FR4, wird das Breitband-Debye-Modell weithin als das genaueste akzeptiert
Mehr zur Kausalität
Beachten Sie, dass wir nur die charakteristische Impedanz einer kausalen Single-Ended-Übertragungsleitung betrachtet haben. Wir haben uns auch nicht den Effekt von Durchkontaktierungen auf Verluste in Kausalmodellen angeschaut. Da nahegelegene Übertragungsleitungen induktiv und kapazitiv koppeln können und beide Arten der Kopplung frequenzabhängig sind, sind die Impedanzen im geraden und ungeraden Modus (und damit die Impedanzen im gemeinsamen und im differentiellen Modus) aufgrund der Dispersion im Substrat auch Funktionen der Frequenz. Zusätzlich zur Modellierung der Dispersion im Substrat erhöht die Kupferrauheit am Rand des Substrats effektiv die Dämpfung in der Leiterbahn, die aufgrund des Skin-Effekts ebenfalls eine Funktion der Frequenz ist. Der typische Weg besteht darin, die Gesamteinfügungsdämpfung auf einer Verbindung umzuschreiben, indem ein Oberflächenrauheitsfaktor (KSR), wie unten definiert, herangezogen wird:
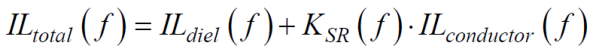
Ich habe in einem verwandten Artikel über einige Aspekte der Modellierung der Kupferrauheit gesprochen. Die Modellierung von Kupferrauheitseffekten als Funktion der Frequenz und das kausale Verhalten von Verbindungen bleibt ein aktives Forschungsgebiet. Ein verbundenes Thema ist das kausale Verhalten eines PDN, da dies für die korrekte Beschreibung der Auswirkungen von Störeinflüssen auf die Leistungsintegrität wichtig ist. Immer mehr gängige Geräte müssen mit höheren Geschwindigkeiten arbeiten, und immer mehr Entwickler arbeiten im Mikrowellen-/mmWellenbereich. Daher werden Tools zur korrekten Beschreibung von Verbindungen als kausale Systeme für die Signalintegrität in Zukunft entscheidend sein.
Die Tools für Impedanzberechnung und Lagenstapel in Altium Designer® behandeln Leiterplatten als kausale Systeme und verwenden das Breitband-Debye-Modell zur Berechnung der Dispersion in Ihrer Leiterplatte. Diese Art von Dienstprogramm ist entscheidend für die Längenabstimmung, das impedanzgesteuerte Routing und die Kontrolle von Verlusten in Leiterplattenverbindungen, insbesondere bei Verbindungen, die mit hoher Geschwindigkeit/hoher Frequenz laufen. Altium Designer enthält außerdem ein integriertes Toolset für die Erstellung von Schaltplänen, die Verwaltung von Bauteilen und die Vorbereitung von Ergebnissen für Ihren Hersteller.
Sie können jetzt eine kostenlose Testversion von Altium Designer herunterladen und mehr über die besten Layout-, Simulations- und Produktionsplanungstools der Branche erfahren. Sprechen Sie noch heute mit einem Altium-Experten, um mehr zu erfahren.